فهم الاختلافات بين مكتبتي لغة بايثون NumPy و Numba
![]()
Photo by Patrick Tomasso on Unsplash
NumPy و Numba هما حزمتان رائعتان متاحتان بلغة بايثون لإجراء عمليات على المصفوفات. كلاهما يعملان بكفاءة على مصفوفات متعددة الأبعاد. في لغة بايثون، تحمل طريقة بناء المتجهات طبيعة ديناميكية. سيؤدي إلحاق قيم جديدة بالمصفوفة إلى زيادة حجم المصفوفة تلقائياً. تعمل مصفوفات NumPy بشكل مختلف حيث تُبنى المصفوفات في أحجام ثابتة. يعني ذلك أن اضافة أو إزالة أي عنصر يقتضي إنشاء مصفوفة جديدة تماماً داخل الذاكرة. في هذه المقالة، نتطلع إلى إيجاد بنية ذات كفاءة تكون فعالة لحل بعض المشاكل البسيطة.
ما هو أساسي عند بدأ النقاش ليس فقط كيفية إنشاء المصفوفة، بل كيفية تطبيق العمليات العلمية المكلفة على هذه المصفوفات، خاصة المصفوفات التي تطلب مسح كافة القيم. الأداء هو الدافع الرئيسي لامتلاك تلك المكتبات عندما نطبق عليها بعض العمليات المكلفة. على سبيل المثال، عندما نقوم بتطوير نماذج تعلم الآلة، خاصة في البيئة التشغيلية، فإننا نقضي قدراً معقولاً من الوقت في تحسين الشفرات التي تنشئ بيانات التدريب باستخدام أي تحويلات مطلوبة أو أي عملية أخرى تتعلق باستخراج وتحويل وتحميل البيانات (ETL). يعد استخدام بعض لغات الآلة البرمجية مثل لغة C أو Fortran أمراً مثالياً، ولكن يتطلب منا إنشاء غلاف "wrapper" هنا وهناك لإعادة العملية التنفيذية للغة بايثون.
ما هو أساسي عند بدأ النقاش ليس فقط كيفية إنشاء المصفوفة، بل كيفية تطبيق العمليات العلمية المكلفة على هذه المصفوفات، خاصة المصفوفات التي تطلب مسح كافة القيم. الأداء هو الدافع الرئيسي لامتلاك تلك المكتبات عندما نطبق عليها بعض العمليات المكلفة. على سبيل المثال، عندما نقوم بتطوير نماذج تعلم الآلة، خاصة في البيئة التشغيلية، فإننا نقضي قدراً معقولاً من الوقت في تحسين الشفرات التي تنشئ بيانات التدريب باستخدام أي تحويلات مطلوبة أو أي عملية أخرى تتعلق باستخراج وتحويل وتحميل البيانات (ETL). يعد استخدام بعض لغات الآلة البرمجية مثل لغة C أو Fortran أمراً مثالياً، ولكن يتطلب منا إنشاء غلاف "wrapper" هنا وهناك لإعادة العملية التنفيذية للغة بايثون.
بناء المصفوفات في بايثون
دعونا نحصل على مثال بسيط: أولاً، سننشئ متجه بسيط بلغة بايثون يحتوي على عشرة ملايين صف. سنتمكن من خلال هذا العدد الكبير ابراز الاختلافات في الأداء بسهولة.# We need to import the random package to fillup the array with some random values.import random
array = []
أنا استخدم IPython ؛ إذا كنت تقوم بتشغيل هذه الشفرات على Jupyter Notebook ، فأوصي باستخدام الأمر "السحري" المدمج (time).
%%time
for i in range(0,10000000):
val = random.randint(0,1000)
array.append(val)
حساب التردد
دعونا نبحث في هذه القائمة عن عدد الصفوف التي تحتوي على القيمة 999؟%%time
freq = 0
for value in array:
if value == 999:
freq = freq + 1
استغرق تنفيذ الأمر على جهازي الخاص 461 مل ثانية ، ووجدت الدالة 10184 مثيلاً للقيمة 999. والآن دعنا نرى كيفية القيام بنفس المهمة باستخدام مصفوفات NumPy.
import numpy as np
# We use the same list created earlier:
np_array = np.array(array)
# To get a sense of the size of the bumpy array, simply call up the function 'shape'
print('The size of the numpy array: ', np_array.shape)
البحث عن عدد الصفوف التي تحتوي على القيمة 999 في مصفوفة NumPy هو سطر واحد فقط من التعليمات
البرمجية:
%%time
result = np.where(np_array == 999)
بالإضافة إلى كتابة بعض القليل من التعليمات لتنفيذ نفس المهمة، استغرق الأمر 12.6 مل ثانية للقيام بنفس مهمة المصفوفة التقليدية.
يرجى ملاحظة أن آلية الفهرسة لمصفوفة NumPy تشبه أي قائمة تقليدية بلغة بايثون.
الآن سنجعل المثال أكثر إثارة للاهتمام من خلال ادخال بعض العمليات الرياضية على قيم المصفوفة. أولاً، سنقوم ببناء ثلاثة متجهات (X ، Y ، Z) من القائمة الأصلية ومن ثم سنقوم بنفس المهمة
باستخدام NumPy.
%%time
def apply_operation_list(array):
# We need to build an X vector from the original array
# The math operations in this function represents some random logic.
x_array = []
for array_v in array:
x_array.append(array_v * 2)
# Building the Y vector
y_array = []
for array_v, x_array_v in zip(array, x_array):
y_array.append(array_v + x_array_v)
# Building the Z vector
z_array = []
for array_v, x_array_v, y_array_v in zip(array, x_array, y_array):
if x_array_v == 0:
z_array.append(0)
else:
z_array.append((array_v - x_array_v ) + y_array_v)
return x_array, y_array, z_array
%%time
x_array, y_array, z_array = apply_operation_list(array)
استغرق تطبيق العملية على القائمة 3.01 ثانية.
دعونا نعيد نفس الوظيفة باستخدام Numpy:
def apply_operation_numpy(array):
# We need to build an X vector from the original array
# The math operations in this function represent some random logic.
x_array = array * 2
# Building the Y vector
y_array = array + x_array
# Building the Z vector
z_array = ( array - x_array ) + y_array
return x_array, y_array, z_array
باستخدام Numpy ، استغرق الأمر 132 مل ثانية فقط.

تعمل مكتبة Numba بشكل مثالي مع العمليات البرمجية المكتوبة بلغة بايثون ويمنحك امتياز استخدام مكتباتك الرياضية المفضلة لديك ولكن تم تجميعها وفقاً لتعليمات الآلة الأصلية [2]. يعد استخدام Numba أمراً بسيطاً ولا يتطلب منك تغيير الطريقة التي تكتب بها الدالة:
Numba
تعمل مكتبة Numba بشكل مثالي مع العمليات البرمجية المكتوبة بلغة بايثون ويمنحك امتياز استخدام مكتباتك الرياضية المفضلة لديك ولكن تم تجميعها وفقاً لتعليمات الآلة الأصلية [2]. يعد استخدام Numba أمراً بسيطاً ولا يتطلب منك تغيير الطريقة التي تكتب بها الدالة:
# Loading the Numba package
# Jit tells numba the function we want to compile
from numba import jit
لاحظ أن كل ما يتعين علينا تغييره مقارنة بالدالة السابقة التي استخدمنا فيها Numpy المحددة أعلاه.
@jit
def apply_operation_numba(array):
# We need to build an X vector from the original array
# The math operations in this function represents some random logic.
x_array = array * 2
# Building the Y vector
y_array = array + x_array
# Building the Z vector
z_array = ( array - x_array ) + y_array
return x_array, y_array, z_array
باستخدام Numba ، استغرق حساب المتجهات الثلاثة 71.5 مل ثانية فقط.
NumPy عبارة عن حاوية هائلة لضغط مساحة المتجه الخاصة بك وتوفير مصفوفات أكثر كفاءة. أهم ميزة هي أداء تلك الحاويات عند إجراء أي معالجة لهذه المتجهات. تم تصميم Numba ، من ناحية أخرى ، لتوفير أكواد بلغة الآلة الأم يعكس وظائف لغة بايثون. يمكن النظر إلى لغة بايثون كغلاف لدوال Numba. من تجربتي ، نستخدم Numba في حالات كانت الوظيفة المراد عملها لا تُدعم من قبل Numpy. أي أن الوظيفة لا تتوفر من هذه المكتبة لمعالجة المتجهات. إذا كانت الوظيفة المخصصة التي تم تنفيذها ليست سريعة بما يكفي في سياقنا ، فيمكن أن تساعدنا Numba في إنشاء هذه الوظيفة داخل مترجم بايثون. هذه هي أيضاً التوصية المتاحة من شرح مكتبة Numba الرسمي.
لا يوضح المثال المقدم في وقت سابق مدى أهمية الفرق؟ هذا صحيح لأننا نبحث فقط عن تكرار قيمة واحدة. دعنا نكرر التجربة عن طريق حساب تكرار جميع القيم المتوفرة في العمود.
في لغة بايثون ، الطريقة الأكثر فعالية لتجنب ما يسمى بالعقدة البرمجية المتداخلة - ذات التكلفة O ^ 2 - هو استخدام الدالة "العداد" (count). باستخدام سطر واحد فقط من الكود ، يمكننا حساب ترددات العمود كاملاً:
أيهما نستخدم؟
"NumPy هي الحزمة الأساسية للحوسبة العلمية مع بايثون. تحتوي بالإضافة إلى أشياء أخرى على كل من: مصفوفات ذات كفاءة متعددة الأبعاد، وظائف (بث) متطورة، وأدوات لدمج أكواد ++C /C و Fortran ، وكذلك الجبر الخطي، وتحويل فورييه ، وقدرات لاستصدار الأرقام العشوائية "[1]NumPy عبارة عن حاوية هائلة لضغط مساحة المتجه الخاصة بك وتوفير مصفوفات أكثر كفاءة. أهم ميزة هي أداء تلك الحاويات عند إجراء أي معالجة لهذه المتجهات. تم تصميم Numba ، من ناحية أخرى ، لتوفير أكواد بلغة الآلة الأم يعكس وظائف لغة بايثون. يمكن النظر إلى لغة بايثون كغلاف لدوال Numba. من تجربتي ، نستخدم Numba في حالات كانت الوظيفة المراد عملها لا تُدعم من قبل Numpy. أي أن الوظيفة لا تتوفر من هذه المكتبة لمعالجة المتجهات. إذا كانت الوظيفة المخصصة التي تم تنفيذها ليست سريعة بما يكفي في سياقنا ، فيمكن أن تساعدنا Numba في إنشاء هذه الوظيفة داخل مترجم بايثون. هذه هي أيضاً التوصية المتاحة من شرح مكتبة Numba الرسمي.
لا يوضح المثال المقدم في وقت سابق مدى أهمية الفرق؟ هذا صحيح لأننا نبحث فقط عن تكرار قيمة واحدة. دعنا نكرر التجربة عن طريق حساب تكرار جميع القيم المتوفرة في العمود.
في لغة بايثون ، الطريقة الأكثر فعالية لتجنب ما يسمى بالعقدة البرمجية المتداخلة - ذات التكلفة O ^ 2 - هو استخدام الدالة "العداد" (count). باستخدام سطر واحد فقط من الكود ، يمكننا حساب ترددات العمود كاملاً:
%%time
count = {x:x_array.count(x) for x in x_array}
ومع ذلك ، اعتماداً على قوة المعالجة لديك ، قد تستغرق هذه الوظيفة ساعات لإكمال 10 ملايين سجل. دعنا نرى بعد ذلك ما يمكن أن تقدمه Numpy:
%%time
x_elements_np, x_counts_np = np.unique(x_array_np, return_counts=True)
استغرق حساب تردد عمود بطول مليون صف 388 مللي ثانية باستخدام Numpy. نقلة كبيرة في الأداء! لاحظ أن هذه الوظيفة يتم تحسينها عن طريق حساب تردد القيم المميزة فقط. هذا مثال يوضح كيف أن استخدام حلقة متداخلة في بيئة بيانات كبيرة أمر غير واقعي.
حتى وقت قريب ، لم تكن Numba تدعم وظيفة np.unique ، ولكن مع ذلك ، لن تحصل على أي فائدة إذا استخدمت مع return_counts. هذا فقط يظهرأنه في بعض الأحيان يمكن أن يكون Numpy هو الخيار الأفضل عند الاختيار.
وأخيرًا ، يوضح الرسمان التاليان أداء وقت التشغيل باستخدام بنية بيانات مختلفة. يمثل المحور س زيادة تدريجية في حجم البيانات من 10000 صف إلى مليار صف.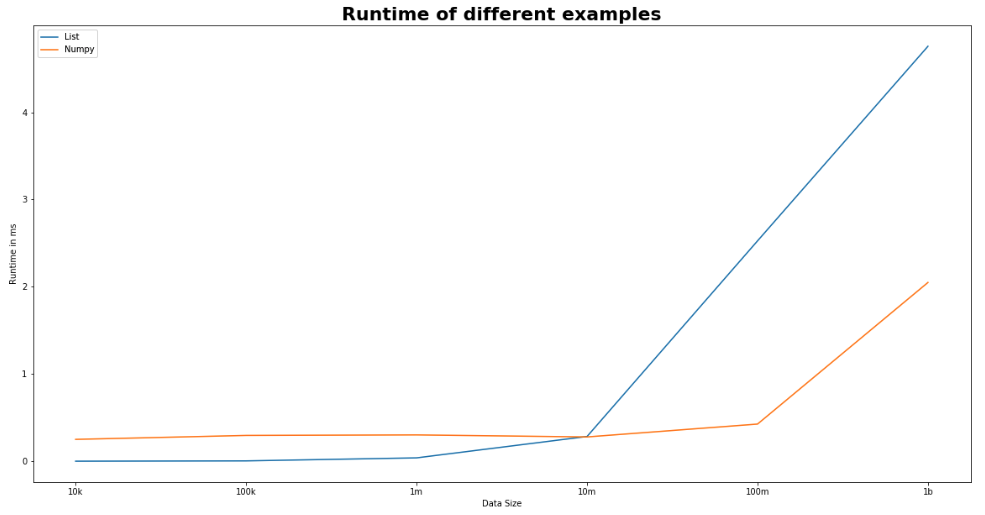 يوضح الشكل التالي أداء Numby مع مكتبة Numba. لاحظ أن الرقم قد يختلف اعتماداً على حجم البيانات. توضح الأرقام في الرسم البياني متوسط تكرار التجربة لخمس مرات.
يوضح الشكل التالي أداء Numby مع مكتبة Numba. لاحظ أن الرقم قد يختلف اعتماداً على حجم البيانات. توضح الأرقام في الرسم البياني متوسط تكرار التجربة لخمس مرات.
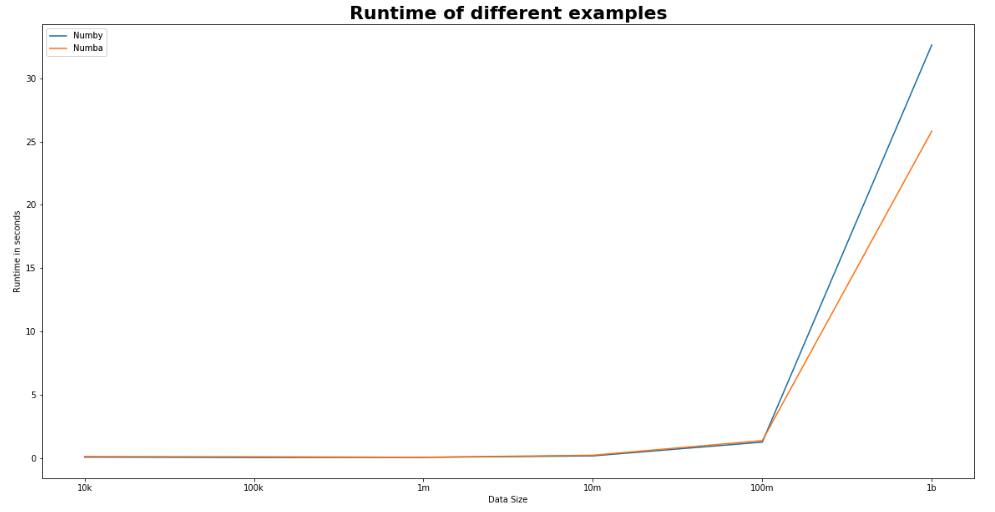
يستخدم المثال المكتوب أدناه بعدين اثنين (أعمدة) فقط بنفس عدد الصفوف كما في المثال السابق.
حتى وقت قريب ، لم تكن Numba تدعم وظيفة np.unique ، ولكن مع ذلك ، لن تحصل على أي فائدة إذا استخدمت مع return_counts. هذا فقط يظهرأنه في بعض الأحيان يمكن أن يكون Numpy هو الخيار الأفضل عند الاختيار.
وأخيرًا ، يوضح الرسمان التاليان أداء وقت التشغيل باستخدام بنية بيانات مختلفة. يمثل المحور س زيادة تدريجية في حجم البيانات من 10000 صف إلى مليار صف.
المزيد من الأمثلة
تحليل القيم المنفردة (SVD)
مثال التكرار هو مجرد تطبيق واحد قد لا يكون كافيا لرسم انطباع شامل ، لذلك دعونا نختار SVD كمثال آخر. SVD هي خوارزمية تعلم غير موجَّه. تسمح الخوارزمية بتفكيك مصفوفة كبيرة إلى منتج من مصفوفات متعددة أصغر في الحجم. SVD لديه العديد من التطبيقات في تعلم الآلة ويستخدم لتقليل الأبعاد. هنا مقال لقراءة المزيد عن هذه الخوارزمية.يستخدم المثال المكتوب أدناه بعدين اثنين (أعمدة) فقط بنفس عدد الصفوف كما في المثال السابق.
from scipy.linalg import svd
# We will consider in this example only two dimensions.
# m x 2
# U: m x r
# s: Diagonal matrix r x r
# VT: n x r
U, s, VT = svd(array_np[:, 0:2])
Sigma = np.zeros((array_np.shape[0], 2))
Sigma[:2, :2] = np.diag(s)
إذا حاولت تشغيل الكود ، فربما تحصل على خطأ مشابه للرسالة التالية: “ValueError: Too large work array required — computation cannot be performed with standard 32-bit LAPACK.”. وذلك لأن التنفيذ الداخلي لـ lapack-lite يستخدم متغيرات من نوع int للفهرس. مع حجم كبير مثل المجموعة المستخدمة ، سيؤدي ذلك بالتأكيد إلى تجاوز الحد التي تستطيع فهرسته. علينا إما تقليل حجم المتجه أو استخدام خوارزمية بديلة. إذا ما حاولنا استخدام وظيفة SVD مع مكتبة Numba ، فلن نحصل على أي مزايا ملحوظة وذلك لان الدالة تستدعي وظيفة LAPACK SVD.
ضرب المصفوفات
ضرب المصفوفات هو مثال آخر يوضح كيف يمكن أن يكون Numba مفيدة لزيادة وقت المعالجة. حتى بدون Cuda ، يمكننا تحقيق أداء أفضل. دعونا نأخذ المثال خطوة بخطوة. كما فعلنا من قبل ، سننفذ وظيفة أولاً باستخدام "قائمة" بايثون.def matrix_multiplication(A,B):
row, col_A = A.shape
col_B = B.shape[1]
result = np.zeros((row,col_B))
for i in range(0,row):
for j in range(0,col_B):
for k in range(0,col_A):
result[i,j] += A[i,k]*B[k,j]
return result
لمعالجة 10 ملايين صف، تكون "القائمة" سريعة جداً في معالجة ضرب المصفوفات. وقت التشغيل هو 1 دقيقة و 7 ثوان فقط. باستخدام Numpy ، استغرق الأمر 95 ثانية للقيام بنفس المهمة.
def matrix_multiplication_numpy(A,B):
result = np.dot(A,B)
return result
%%time
result = matrix_multiplication_numpy(array_np, array_np)
الآن بعد استبدال Numby بـ Numba ، قمنا بتقليل عمليات الضرب المكلفة من خلال وظيفة بسيطة أدت إلى 68 ثانية فقط أي تقليل الوقت بنسبة 28٪.
@jit
def matrix_multiplication_numba(A, B, result):
for i in range(result.shape[0]):
for j in range(result.shape[1]):
tmp = 0.
for k in range(A.shape[1]):
tmp += A[i, k] * B[k, j]
result[i, j] = tmp
توضح الشكل البياني التالي أداء ضرب المصفوفة باستخدام قائمة Python ، مع Numpy ، وباستخدام مكتبة Numpy.
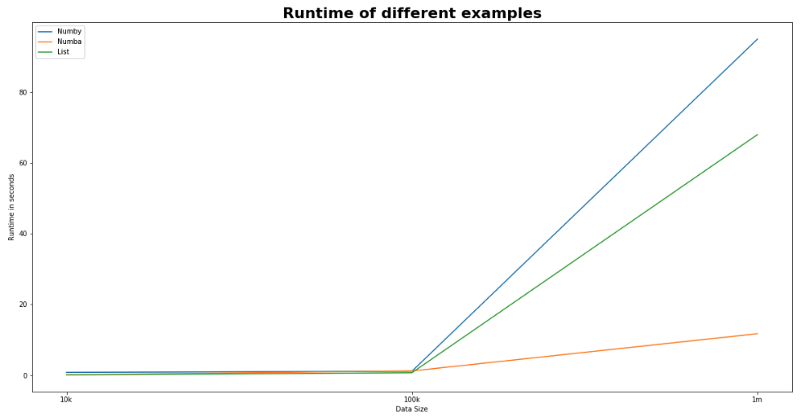 تم تشغيل الأمثلة المقدمة في هذه المدونة على جهاز MacBook Pro مقاس 15 بوصة 2018 وحجم الذاكرة 16 جيجابايت واستخدام توزيعة أناكوندا. يمكن العثور على التعليمات البرمجية المستخدمة في هذه الأمثلة في مستودع Github
الخاص بي. يمكن تحسين الأداء باستخدام بيئة GPU ، والتي لم يتم أخذها في الاعتبار في هذه المقارنة.
تم تشغيل الأمثلة المقدمة في هذه المدونة على جهاز MacBook Pro مقاس 15 بوصة 2018 وحجم الذاكرة 16 جيجابايت واستخدام توزيعة أناكوندا. يمكن العثور على التعليمات البرمجية المستخدمة في هذه الأمثلة في مستودع Github
الخاص بي. يمكن تحسين الأداء باستخدام بيئة GPU ، والتي لم يتم أخذها في الاعتبار في هذه المقارنة.
المراجع
[1] Official NumPy website, available online at https://numpy.org [2] Official Numba website, available online at http://numba.pydata.org
