تعلم الآلة - أساليب أخذ العينات
![]()
Photo by Luke Chesser on Unsplash
لطالما ارتبط مفهوم العينات بالعملية البحثية التي تتطلب اختبار صحة أو قبول فرضيات يتعذر اختبارها على شريحة واسعة أو باستخدام أمثلة غزيرة. في تعلم الآلة، سرعان ما نقفز للسؤال عن ماهية البيانات المستخدمة وأحجام توفرها. ستسلط هذه المقالة على الحالات التي نلجأ فيها عند بناء نماذج تعلم الآلة للأخذ بالعينات وتدريب النموذج على عينة من البيانات عوضاً عن كاملها. سنتحدث أيضاً عن أكثر الطرق صحةً سواءً لأغراض التدريب أو الاختبار وما يتعلق بذلك من أساليب علمية.
عندما يطرح موضوع الأخذ بالعينات يتبادر العديد من المهتمين ببناء نماذج تعلم الآلة للتحدث عن توزيع البيانات لمجموعات تختص كل منها لمهمة محددة: التدريب، التحقق من التعلم، أو اختبار النموذج. لا شك أن هذه الخطوات تحتاج لأساليب أخذ العينات لكن السؤال الأهم الذي لا يجب أن نتغافل عنه، ماذا لو كان استخدام كامل البيانات في هذه العملية غير ممكن. أي أن كثافة البيانات الممكن استخدامها محدودة. أهمية أخذ العينات لا يقل أهمية عن هندسة النموذج، حيث وجود خلل في تمثيل البيانات يهبط بدقة أداء النموذج أو بقدرتها على استيعاب أمثلة جديدة خارج نطاق العينة.
تعذُر استخدام جميع البيانات في التدريب يأتي في عدة صور، إما لعدم توفر الإمكانيات لمعالجتها أو عدم إمكانية اسكانها في الذاكرة المؤقتة. على سبيل المثال: لنفرض أن تدريب النموذج لتطبيق معين يجب أن يتم في ثوان، وعليه اللجوء لأخذ عينات أمر أساسي ومنه يجب أن نصل لآلية لأخذ أفضل الصور التي تمثل البيانات الحقيقية. نقصد بالصور هنا تلك العينات التي تصور لنا خصائص البيانات الكبيرة بشكل مختزل مع الحفاظ على خصائصها الإحصائية.
من الجانب الآخر الوقت المستغرق لبناء النموذج يحتم علينا اللجوء لأخذ عينات أو اجتزاء جزء من البيانات الكلية لغرض التدريب. في كثير من الأحيان يتطلب على مهندسي نماذج تعلم الآلة بناء نموذج لا يستغرق تدريبه إلا دقائق معدودة. هذا السبب يعود لتطلع الشركات لاستمرارية تعلم النماذج و استيعاب حقائق جديدة عوضاً عن بناء نموذج واحد مكلف. على سبيل المثال، توقع المبيعات لا يعتمد على بيانات جمعت في السنوات الماضية فقط بل يعتمد على البيانات المتدفقة بشكل مستمر. وفي سياق آخر من الممكن الاكتفاء بنموذج واحد مكلف كالنماذج اللغوية التي لا تحتاج لإعادة التدريب بشكل مستمر وتكون أساليب أخذ العينات ليس بسبب الحجم فقط ولكن لأسباب أخرى سنذكرها في هذا المقال.

في واقع تعاملنا مع نماذج تعلم الآلة من الطبيعي أن نتوقع وجود خلل في تمثيل البيانات ذلك يعود للطريقة التي جمعت بها. لو أردنا بناء نموذج يتوقع نسبة قبول طالب ما في كلية الطب بناء على أدائه الدراسي فإن المجتمع الذي تمثله البيانات المجمعة يجب أن يكون متوازناً. فلا يمكن دراسة أداء الطلاب دون الطالبات أو أن تمثيل الطلاب يفوق عدد تمثيل الطالبات و العكس صحيح. بالاضافة إلى أهمية الأخذ بعين الاعتبار أخذ عينات من مدراس مختلفة وغيرها. وجود أي خلل في تمثيل هذه البيانات حتماً سيؤثر على أداء النموذج و قدرته على استيعاب حالات جديدة تحمل خصائص احصائية مختلفة عن ما تعلمته الآلة أثناء التدريب.
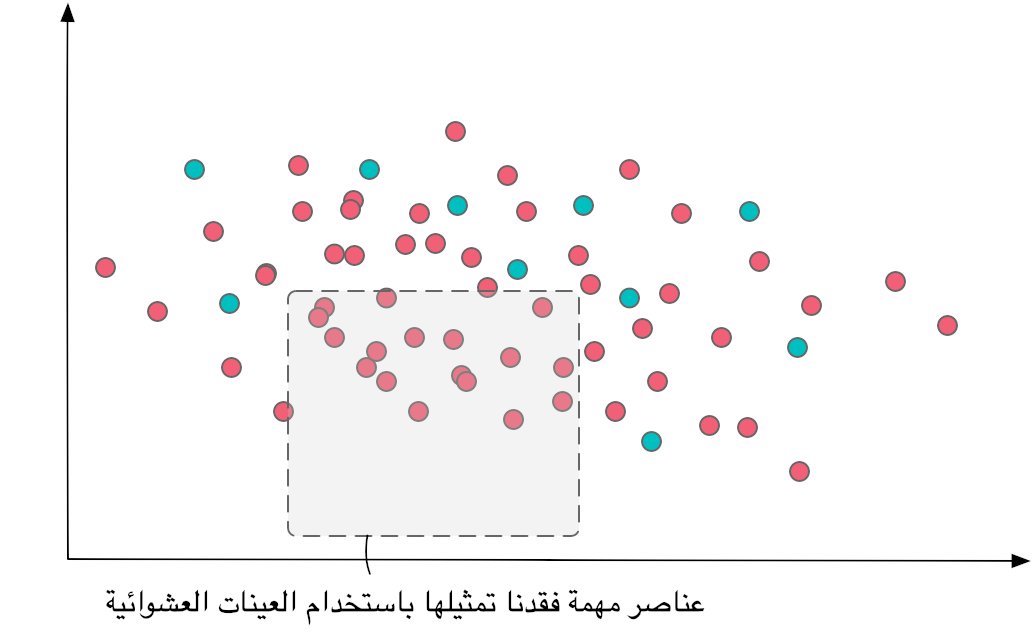
النقاط المضاءة باللون الأخضر تعبر عن عينات محددة عشوائيا بينما المضاءة باللون الأحمر تمثل البيانات التي لم تستخدم في تمثيل العينة. المتجه س والمتجه ص يمكن أن يمثل أي بعد تمثله هذه البيانات. كما تبين الصورة، من المحتمل أن نفقد تمثيل أجزاء مهمة من توزيعة البيانات قد تؤثر على أداء النموذج خصوصاً مع صغر حجم العينة.
من الطرق المستخدمة لتطبيق آلية أخذ عينات عشوائية ما يسمى ب (Reservoir Sampling). هذه الخوارزمية العشوائية تمكننا من اختيار نافذة داخل البيانات من توزيعة البيانات الأساسية عن طريق اختيار أرقام عشوائية كما هو موضح في الصورة التالية: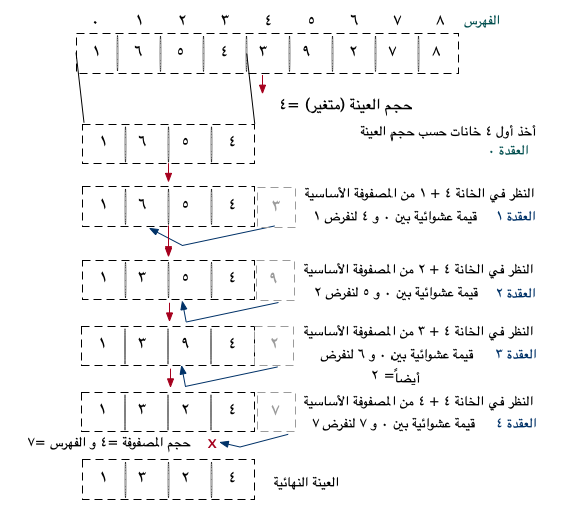
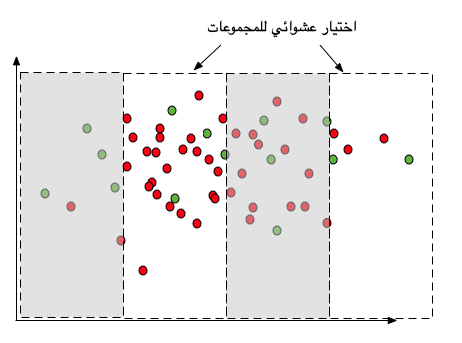
الطرق الإحصائية تقترح أسلوبين في التعامل مع هذه الطريقة إما أخذ المجموعة كاملة بكل عيناتها أو العودة للاختيار عينات عشوائية من هذه المجموعات.
يتم تقسيم البيانات لأغراض التدريب لمجموعتين تشكل بيانات التدريب فيها ٨٠٪ من مجمل عدد العينات و يستخدم ٢٠٪ المتبقية لأغراض اختبار أداء النموذج. ثم يعاد تقسيم بيانات التدريب باستخدام نفس القاعدة (٨٠-٢٠) لنحصل على مجموعتين: مجموعة المدخلات للتدريب ومجموعة التحقق والتي تعتمد عليها الخوارزميات في تتبع مراحل تعلم النموذج و كذلك في ضبط معاملات النموذج.
الاكتفاء بهذا التقسيم غير كافٍ، ذلك يعود للأسباب التالية: أولاً احتمالية أن توزيع البيانات العشوائي بسبب بمصادفة مكنت النموذج من بذل أداء تنبؤ عالي جداً يختلف عن فيما لو أعيدت خطوة التدريب و الاختبار. و السبب الآخر أن عدد العينات المستخدمة غير كاف لتعلم النموذج. وفي هذه الحالتين نلجأ لما يسمى ب (k-fold). مفهوم (k-fold) يتيح لنا تقسيم المجاميع إلى عدد (k) بحيث أن كل مجموعة من هذه المجاميع تُستخدم للتحقق و يعاد المتبقي منها للتدريب و تعاد الكرة بمجموعة أخرى للتحقق لا تتقاطع مع سابقتها و يستخدم المتبقي منها في التدريب وهكذا.
وفي الختام أريد أن أنوه أن الطرق الإحصائية تزخر بالعديد من الأساليب العلمية المتبعة لأخذ العينات بطريقة غير عشوائية كالعينات العرضية أو العينات القصدية التي تهتم بشريحة معينة من البيانات و غيرها. لا شك بأهمية هذه الأساليب بحثياً في حالات مختلفة لكن استخدامها محدود في مجال تعلم الآلة نظراً لاننا دائماً ما نبحث عن تمثيل حقيقي للبيانات من خلال أخذ عينات تتسم بالشمولية.
عندما يطرح موضوع الأخذ بالعينات يتبادر العديد من المهتمين ببناء نماذج تعلم الآلة للتحدث عن توزيع البيانات لمجموعات تختص كل منها لمهمة محددة: التدريب، التحقق من التعلم، أو اختبار النموذج. لا شك أن هذه الخطوات تحتاج لأساليب أخذ العينات لكن السؤال الأهم الذي لا يجب أن نتغافل عنه، ماذا لو كان استخدام كامل البيانات في هذه العملية غير ممكن. أي أن كثافة البيانات الممكن استخدامها محدودة. أهمية أخذ العينات لا يقل أهمية عن هندسة النموذج، حيث وجود خلل في تمثيل البيانات يهبط بدقة أداء النموذج أو بقدرتها على استيعاب أمثلة جديدة خارج نطاق العينة.
تعذُر استخدام جميع البيانات في التدريب يأتي في عدة صور، إما لعدم توفر الإمكانيات لمعالجتها أو عدم إمكانية اسكانها في الذاكرة المؤقتة. على سبيل المثال: لنفرض أن تدريب النموذج لتطبيق معين يجب أن يتم في ثوان، وعليه اللجوء لأخذ عينات أمر أساسي ومنه يجب أن نصل لآلية لأخذ أفضل الصور التي تمثل البيانات الحقيقية. نقصد بالصور هنا تلك العينات التي تصور لنا خصائص البيانات الكبيرة بشكل مختزل مع الحفاظ على خصائصها الإحصائية.
تعذر استيعاب البيانات الكبيرة
البيانات تتسم عادة بأحجام مختلفة حسب سياق التطبيق أو النظام الذي يستخلصها من البيئة التشغيلية. وعند رغبتنا في بناء نماذج تعلم الآلة فإن امكانية استيعاب هذه البيانات مبني على توفر بنية تحتية تستطيع استيعاب كمية كبيرة من هذه البيانات. اسكان هذه البيانات في الذاكرة ومعالجتها أمر ليس بالسهولة ووفي الواقع فإن البيئة التشغيلية تحتم علينا التعامل مع عدد محدد من الأحجام.من الجانب الآخر الوقت المستغرق لبناء النموذج يحتم علينا اللجوء لأخذ عينات أو اجتزاء جزء من البيانات الكلية لغرض التدريب. في كثير من الأحيان يتطلب على مهندسي نماذج تعلم الآلة بناء نموذج لا يستغرق تدريبه إلا دقائق معدودة. هذا السبب يعود لتطلع الشركات لاستمرارية تعلم النماذج و استيعاب حقائق جديدة عوضاً عن بناء نموذج واحد مكلف. على سبيل المثال، توقع المبيعات لا يعتمد على بيانات جمعت في السنوات الماضية فقط بل يعتمد على البيانات المتدفقة بشكل مستمر. وفي سياق آخر من الممكن الاكتفاء بنموذج واحد مكلف كالنماذج اللغوية التي لا تحتاج لإعادة التدريب بشكل مستمر وتكون أساليب أخذ العينات ليس بسبب الحجم فقط ولكن لأسباب أخرى سنذكرها في هذا المقال.
عدم توازن البيانات
في واقع تعاملنا مع نماذج تعلم الآلة من الطبيعي أن نتوقع وجود خلل في تمثيل البيانات ذلك يعود للطريقة التي جمعت بها. لو أردنا بناء نموذج يتوقع نسبة قبول طالب ما في كلية الطب بناء على أدائه الدراسي فإن المجتمع الذي تمثله البيانات المجمعة يجب أن يكون متوازناً. فلا يمكن دراسة أداء الطلاب دون الطالبات أو أن تمثيل الطلاب يفوق عدد تمثيل الطالبات و العكس صحيح. بالاضافة إلى أهمية الأخذ بعين الاعتبار أخذ عينات من مدراس مختلفة وغيرها. وجود أي خلل في تمثيل هذه البيانات حتماً سيؤثر على أداء النموذج و قدرته على استيعاب حالات جديدة تحمل خصائص احصائية مختلفة عن ما تعلمته الآلة أثناء التدريب.
ما هي الطرق المناسبة؟
العينات العشوائية
العينات العشوائية فعالة غالباً وتعكس الشكل التمثيلي للبيانات الأساسية بشكل جيد وذلك بسبب إعطاء كل عينة نفس احتمالية الفرصة في الاختيار دون أي انحياز أو تدخل في تشكيل توزيعات هذه العينات. نلجأ للعشوائية في جميع الحالات التي لا يتطلب النموذج فيها على أي خصائص معينة في تشكيل البيانات المستهدفة ويترك للعينات أن تترشح بشكل عشوائي. نلجأ لهذا الأسلوب كذلك في الحالات التي يتعذر علينا فهم الخصائص المستهدفة في العينات التي يجب علينا تجميعها لبناء النموذج. العشوائية تضفي فعالية كما ذكرنا بسبب توحيد احتمالية التمثيل لكنها في حد ذاتها ليست مثالية في كل الحالات كما تبينه الصورة التالية.النقاط المضاءة باللون الأخضر تعبر عن عينات محددة عشوائيا بينما المضاءة باللون الأحمر تمثل البيانات التي لم تستخدم في تمثيل العينة. المتجه س والمتجه ص يمكن أن يمثل أي بعد تمثله هذه البيانات. كما تبين الصورة، من المحتمل أن نفقد تمثيل أجزاء مهمة من توزيعة البيانات قد تؤثر على أداء النموذج خصوصاً مع صغر حجم العينة.
من الطرق المستخدمة لتطبيق آلية أخذ عينات عشوائية ما يسمى ب (Reservoir Sampling). هذه الخوارزمية العشوائية تمكننا من اختيار نافذة داخل البيانات من توزيعة البيانات الأساسية عن طريق اختيار أرقام عشوائية كما هو موضح في الصورة التالية:
العينات الطبقية
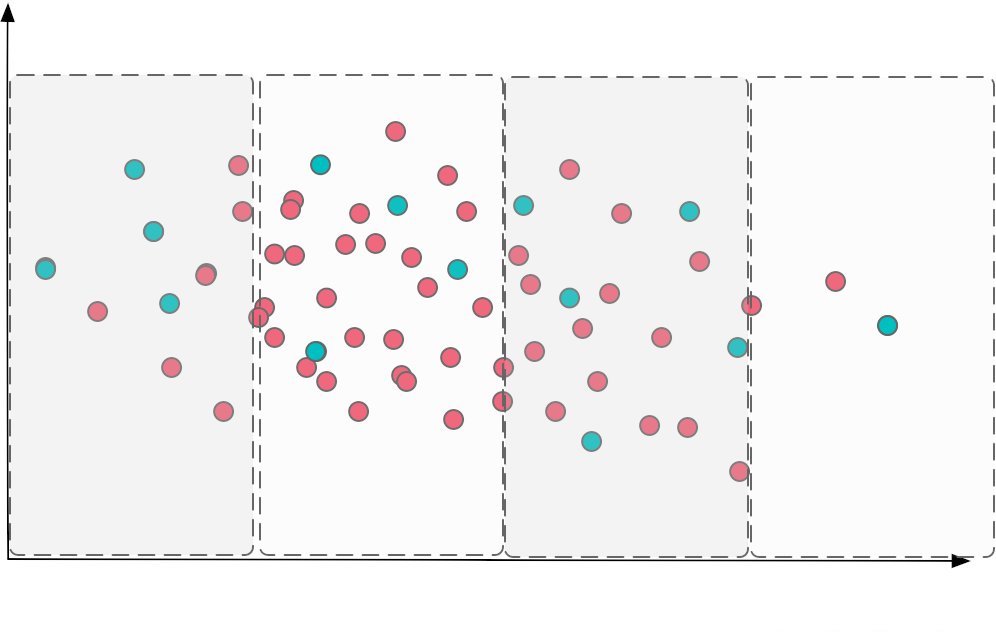
من الحلول التي انصح بالاطلاع عليها خصوصاً في تمثيل البيانات لغرض بناء نماذج الآلة أخذ العينات الطبقية. تأخذ العينات الطبقية (Stratified Sampling) قوتها من مفهوم تشكيل مجموعات بيانية ومن ثم أخذ عينات عشوائية من كل مجموعة بشكل متوازن. فهي تتسم بالتصنيف المسبق مع الحفاظ على التحلي بالعشوائية في أخذ العينات من كل مجموعة كما في الصورة التالية.عينات المجاميع العشوائية
طريقة (Cluster Random Sampling) تشبه الطريقة الطبقية بإضافة العشوائية في اختيار المجموعة نفسها ويطلق عليها في بعض الكتب العينات العنقودية.الطرق الإحصائية تقترح أسلوبين في التعامل مع هذه الطريقة إما أخذ المجموعة كاملة بكل عيناتها أو العودة للاختيار عينات عشوائية من هذه المجموعات.
الطريقة الممنهجة
هناك طرق لأخذ العينات تعتمد على عملية ممنهجة تعتمد على نظام متسلسل في الاختيار. لإعطاء مثال لتوضيح الفكرة: عند بناء بيانات لتدريب نموذج لتوقع أسعار الأسهم في سوق التداول، فقد يكون من المهم أخذ قراءة أسعار الشركات عند فتح السوق و عند غلق السوق وأخرى تمثل متوسط سعر المضاربة بين فتح و إغلاق السوق. هذه العملية الممنهجة هي في الحقيقة أخذ عينات من أسعار المضاربة في سوق الأسهم بناء على التسلسل الزمني.العينات المبنية على الحصص
بعض النماذج يجب أن نعير الاهتمام فيها إلى سياق القرار المتوقع التنبؤ به أو القيم المراد للنموذج أن يتعلمها. على سبيل المثال، هناك نماذج حقيقية انتشر مؤخراً انحيازها لجنس المتقدم للحصول على بطاقة ائتمانية. الشركة اصدرت بطاقات ذات حد ائتماني منخفض لمتقدمة أنثى تحمل نفس العمر و مستوى الدخل لمتقدم آخر رجل. هذا الانجياز يكون مسببه خلل في توازن عناصر مهمة مثل العمر أو الجنس أو المدينة المقيم فيها المتقدم وغيرها. لحل هذه المشكلة، نلجأ لتقسيم البيانات لحصص متسواية من العينات يكون التمثيل فيها متجانساً. مثال آخر، لو أردنا لنموذج أن يتعلم تصنيف رسائل البريد الإلكترونية إلى رسائل مزعجة وغير مزعجة فإن تمثيل العينات يجب أن يكون متجانساً بحيث لا يغلب الغير مزعج منها على الآخر و العكس صحيح.إعادة التوازن
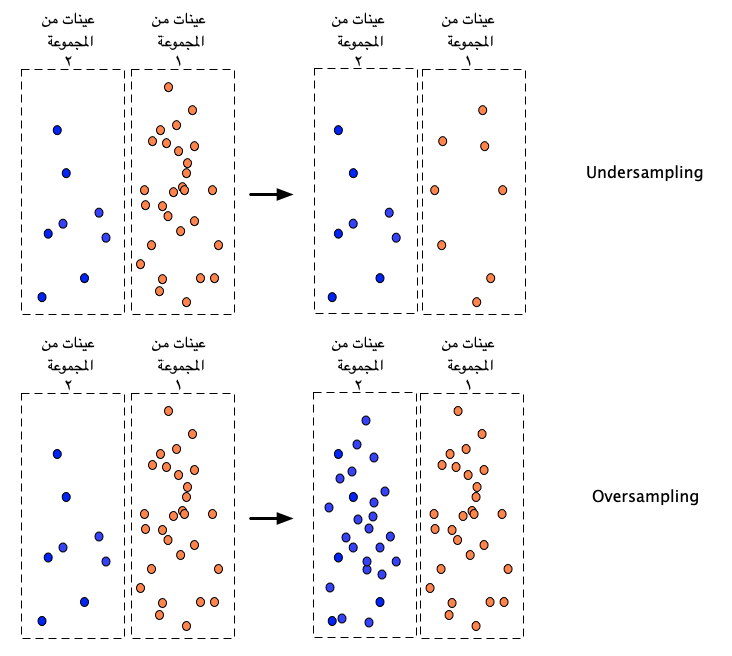
في مجال تعلم الآلة نتعامل مع اختلال التوازن الذي تمثله العينات بطريقتين: الأولى خفض التمثيل (Undersampling) والأخرى رفع التمثيل (Oversampling) كما في الصورة التالية:توزيع العينات أثناء بناء النموذج
كما ذكرت في بداية هذا المقال، الحديث عن أخذ العينات لبيانات التدريب وتوزيعها لمجموعات لكل مرحلة في قناة بناء النموذج هي الحاجة الأكثر شيوعاً لحاجتنا لأخذ العينات. قبل أن نتطرق للتفاصيل يجب أن أوضح أن كل الطرق السابقة تأتي في تمثيل البيانات قبل هذه الخطوة وأن تقسيم البيانات لبيانات للتدريب (Training Set)، أو التحقق من التعلم(Validation Set)، أو اختبار النموذج (Testing Set) هي بعد الوصول لتمثيل بياني مناسب للتعلم الآلي بالإجمال.يتم تقسيم البيانات لأغراض التدريب لمجموعتين تشكل بيانات التدريب فيها ٨٠٪ من مجمل عدد العينات و يستخدم ٢٠٪ المتبقية لأغراض اختبار أداء النموذج. ثم يعاد تقسيم بيانات التدريب باستخدام نفس القاعدة (٨٠-٢٠) لنحصل على مجموعتين: مجموعة المدخلات للتدريب ومجموعة التحقق والتي تعتمد عليها الخوارزميات في تتبع مراحل تعلم النموذج و كذلك في ضبط معاملات النموذج.
الاكتفاء بهذا التقسيم غير كافٍ، ذلك يعود للأسباب التالية: أولاً احتمالية أن توزيع البيانات العشوائي بسبب بمصادفة مكنت النموذج من بذل أداء تنبؤ عالي جداً يختلف عن فيما لو أعيدت خطوة التدريب و الاختبار. و السبب الآخر أن عدد العينات المستخدمة غير كاف لتعلم النموذج. وفي هذه الحالتين نلجأ لما يسمى ب (k-fold). مفهوم (k-fold) يتيح لنا تقسيم المجاميع إلى عدد (k) بحيث أن كل مجموعة من هذه المجاميع تُستخدم للتحقق و يعاد المتبقي منها للتدريب و تعاد الكرة بمجموعة أخرى للتحقق لا تتقاطع مع سابقتها و يستخدم المتبقي منها في التدريب وهكذا.
وفي الختام أريد أن أنوه أن الطرق الإحصائية تزخر بالعديد من الأساليب العلمية المتبعة لأخذ العينات بطريقة غير عشوائية كالعينات العرضية أو العينات القصدية التي تهتم بشريحة معينة من البيانات و غيرها. لا شك بأهمية هذه الأساليب بحثياً في حالات مختلفة لكن استخدامها محدود في مجال تعلم الآلة نظراً لاننا دائماً ما نبحث عن تمثيل حقيقي للبيانات من خلال أخذ عينات تتسم بالشمولية.
